8 - Binary Search Trees

8.1 - Binary Search Trees

• Binary Tree = A herarchical structure consisting of a root element with two distinct binary trees (right and left).
• Length = Number of edges in the path.
• Depth = The length of the path from the root to the specified node.
• Level = The set of nodes at a given depth.
• Siblings = Nodes that share the same parent.
• Leaf = A node without children.
• Height = The number of nodes from the root node to the most deepest node.
• Binary Search Tree (BST) = Items hich are lower than the current node is placed on the left subtree, items higher then the current node is palced on the right subtree.

• A node is usually defined as follows:

  • class TreeNode<E> {
        protected E element;            //Current element
        protected TreeNode<E> left;     //Left subtree
        protected TreeNode<E> right;    //Right subtree
    
        public TreeNode(E e) {
            element = e;
        }
    }
    

• Searching for an element is done by comparing the current element (which we are looking at) with the target element (for which you are looking for).

  • If the target element is smaller then the current element, go to the left subtree.
  • If the target element is bigger then the current element, go to the right subtree.
  • If the target element is equal to the current element, it has been found.

• Inserting an element is done at the first parent which does not have any childs.

  • While finding the parent the tree needs to be followed by comparing the element we want to insert to the one we have selected as parent.
  • Moving down while keeping the rules of searching (see above) applied.

• Removing an element is done by finding the element, and then if the node has a child reconnect that back to the tree.

  • If the element we want to remove has a left child (see image in next paragraph):
    • Replace the element to be removed with his most right (grand) child of his left subtree.
    • Make any children of that most right element, children of that most rights parent.
    • Example:
      • We want to remove 60, he has no parent :(.
      • He has child 55 and 100.
      • The most right (grand)child from the left tree of 60 is 59.
      • We replace 60 with 59.
      • Any childs of 59 we make childs of the parent of 59 (57)
  • If the element we want to remove has a right child (see image in next paragraph):
    • Connect the right child of the element to be removed to the parent of that element. At the position the element to be removed was.
    • Example:
      • We want to remove 57, his parent is 55.
      • He has child 59.
      • Replace 57 with 59, and delete 57.
  • If the element we want to remove has a left and a right child:
    • Only do the left child removal process. Right subtree stays attached the same.
  • If the element we want to remove has no childs (see image in next paragraph):
    • Just take it out already.
    • Example:
      • We want to remove 101, his parent is 107.
      • We delete 101.

• You can use recusion to display binary trees.

• Using a Huffman coding scheme. Codes for characters are constructed based on the occurrence of characters in the text using a binary tree. (pg 959)

8.2 - Tree Traversal

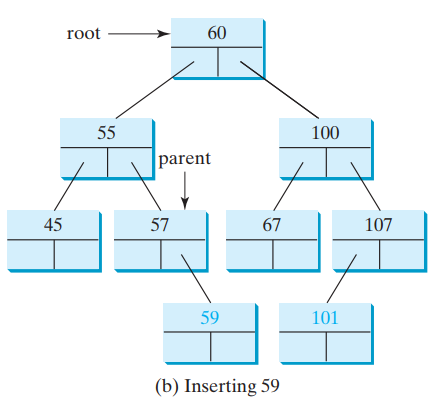
• Tree Traversal = The process of visisiting each node in the tree exactly once.

• InOrder = Left - Current - Right (45, 55, 57, 59, 60, 67, 100, 101, 107)

• PostOrder = Left - Right - Current (45, 59, 57, 55, 67, 101, 107, 100, 60)

• PreOrder / Depth-First = Current - Left - Right (60, 55, 45, 57, 59, 100, 67, 107, 101)

• Breadth-Firist = Per level, top to bottom. (60, 55, 100, 45, 57, 67, 107,59, 101)