1 - Recursion

1.1 - Introduction

• Recursion = A technique that leads to elegeant solutions to problems that are difficult to program using simple loops.
  • Recursion enables you to create an intuitive, straightforward, simple solution to a problem.
  • Disadvantages:
    • Requires more time and memory to run then using a loop.
• VLSI = Very large-scale integration design.
• Recursive Methods = Methods that invoke themselves.
  • Characteristics:
    1. The method needs to have an if-else or switch statement implemented to lead to different cases.
    2. The method needs to have one or more base-cases, used to stop recurison.
       • Base case/stopping case = The simpelest case that the method can solve. If this is accessed, it will not invoke itself but give back a result. And starts terminating the recursive method.
       • Without a stopping case, the method will be run infinite. Which will result in an StackOverflowException.
    3. Each call of the method needs to reduce the original problem, bringing it increasingly closer to a base case until it becomes that.
       • Subproblem = A smaller or simpler problem then the original problem.
       • Recursive Call = When an method invokes itself, but with different arguments. This can lead to more recursive calls, because the subproblems will create more subproblems.
• Recursive Helper Method = A recursive method with the same function as the original problem, but with other parameters.

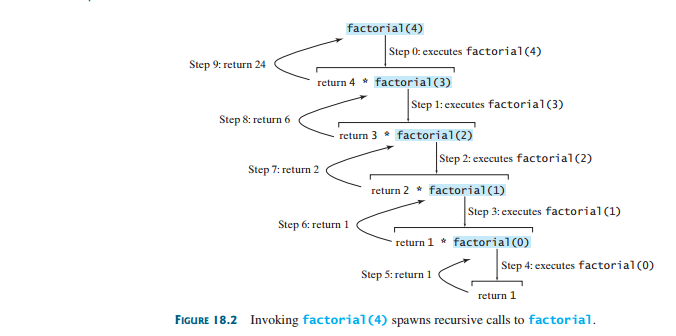
• Direct Recursion = When a method invokes itself.
• Indirect Recursion = When a method invokes other methods which in turn invokes the original method. (A->B->C->A)
• Tail Recursion = When there are no pending operations after completing the method.
  • This reduces memory needed for the recursive method.
  • Non-tail recursion methods, can be converted to tail recurion methods by using auxillary parameters.

1.2 - Recursion VS Iteration

• When using a loop, the loopbody controls the loop. A method calls itself repeatedly, an selection statement must exist to end the recursion.
• Recursion bears extential overhead. All the methods variables and parameters need to be stored into memory. Also the managing of the memory requires time.
• Use recursion when a problem requires a simple, clear solution.
• Rule of thumb: Use the approach which lies closest to the natural solution of the problem.
• If concerned about performance, avoid recursion.

1.E - Used Examples

• Pg 706 = H-tree problem (Creating a screen in which each ends of the H another H is placed on the midbeam)
• Pg 706 = Computing Factorials ( 5! = 5*4*3*2*1)
• Pg 709 = Computing Fibonacci Numbers (0,1,1,2,3,5,8,13,21 etc. Summing the previous two numbers to create the next)
• Pg 713 = Is a word a Palindrome (Words that can be read backwards, and forwards. For example: racecar)
• Pg 715 = Selection Sort (Sort an arrray from smallest to highest)
• Pg 716 = Binary Search
• Pg 717 = Directory Size
• Pg 719 = Tower of Hanoi (Move disks from A to C with B in between. Only stacking smaller on larger disks)
• Pg 722 = Fractals (Sort of triangles)