5 - Developing Efficient Algorithms

5.1 - Introduction

• Algorithm design = Develop a mathematical process for solving a problem.
• Algorithm analysis = Predict the performance of an algorithm.
  • Extecution time not a good measure:
    • Execution time depends on overall system load. (Other system tasks take resources as well)
    • Execution time depends on specific input. (One can be solved easier bij A then by B)
• The big O notation = A function for measuring algorithm time complexity based on the input size.
  • Can be used for both time complexity and space complexity (RAM usage).
  • Ignore multiplicative(3 in n*3) constants.
  • Ignore nondominating terms (-1 in n-1, when n tripples) in the algorithm.
  • Approximates the effect of a change on the size of the input. (growth-rate).
  • When two algorithms have the same complexity, it does not mean that they are equally efficient.
• Growth-rate = How fast does the execution time increase as the imput size increases.
  • Displayed in order of magnitude (n).
• Best-case input = Input that results into the shortest execution time.
• Worst-case input = Input that results into the longest execution time.
  • Verry usefull, because no input can be slower then the worst-case input.
• Average-case analysis = Determining the average amount of time among all possible inputs of the same size.
  • Ideal but difficult to perform, because determining all possiblities for some problems is impossible.
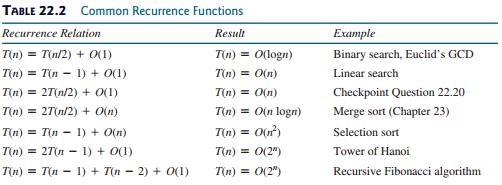
• Recurrence Relations =
  • 
• Dynamic Programming = The process of solving subproblems, then combining the solutions ofthe subproblems to obtain an overall solution.
  • By storing the solutions for subproblems, so recursion can be avoided.
• Prime Number = An number that can only be divided by 1 or by itself.
• Backtracking approach = Searches for a candidate solution incrementally, abandoning a solution as soon as it determines that the candidate cannot possibly be a valid solution, and then looks for a new candidate.

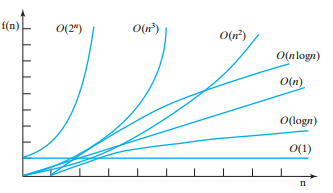
5.2 - Big(O) sizes

• Ordered from lowest complexity to highest complexity
  • O(1) > Input size does not matter, processing time stays the same.(Constant time)
  • O(log(n)) > Processing time gets slightly more when the input doubles. (Logarithmic time)
  • O(sqrt(n)) > .
  • O(n) > Processing time grows evenly with the input size. (Linear time)
  • O(n log(n)) > Log-Linear time
  • O(n^2) > Quadratic time
  • O(n^3) > Qubic time
  • O(2^n) > Exponential time

• Programming examples and their complexity

  • O(n)

    • //1
      for (int i = 1; i <= n; i++) { 
          k = k + 5
      }
      //2
      for (int i = 1; i <= n; i++) {
          for (int j = 1; j <= 20; j++) {
              k = k + i + j;
          }
      }
      //3
      for (int j = 1; j <= 10; j++) {
          k = + 4;
      }
      for (int i = 1; i <= n; i++) {
          for (int j = 1; j <= 20; j++) {
              k = k + i + j;
          }
      }
      //4
      if (list.contains(e)){
          System.out.println(e);
      }
      else {
          for (Object t: list) {
              System.out.println(t)
          }
      }
      //5
      result = 1
      

  • O(n^2)

    • //1
      for (int i = 1; i <= n; i++) {
          for (int j = 1; j <= n; j++) {
              k = k + i + j;
          }
      }
      
      //2
      for (int i = 1; i <= n; i++) {
          for (int j = 1; j <= i; j++) {
              k = k + i + j;
          }
      }
      

  ---

5.E - Used Examples

• Pg 828 = Binary Sort (O(log n))
• Pg 828 = Selection Sort (O(n^2))
• Pg 828 = Tower of Hanoi (O(2^n))
• Pg 831 = Fibonacci using Recursive Programming (O(2^n))
• Pg 832 = Fibonacci using Dynamic Programming (O(n))
• Pg 833 = Greatest Common Divisors (O(n)
• Pg 835 = Greatest Common Divisors using Euclid (O(log(n)))
• Pg 838 = Finding primenumbers by checking the divisors up to sqrt(n) (O(n sqrt(n)))
• Pg 839 = Finding prime numbers by checking the prime divisors up to sqrt(n) (O(n sqrt(n) / log(n)))
• Pg 842 = Finding prime numbers by using the Sieve Of Eratosthenes (O(n sqrt(n) / log(n)))