6 - Sorting

6.1 - Introduction

• Why study sorting:
  • Sorting algorithms illustrate many creative approaches to problem solving, which could be applied to other problems.
  • Sorting algorithms are good for practicing fundamental programming techniques (loops, methods, arrays, statement etc)
  • Sorting algorithms are excellent examples to demonstrate algorithm performance.
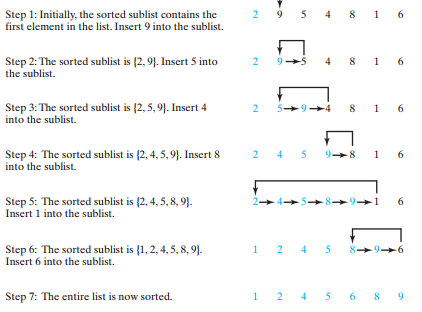
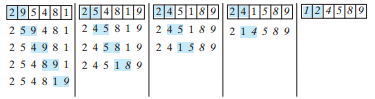
• Insertion Sort = Sorting of a list of values by repeatingly inserting a new element into a sorted sublist until the whole list is sorted. (O (n^2))
  • 
• Bubble Sort = Sorting of a list of values by successively swapping the neighboring elements if they are not in order (O (n^2))
  • 
• Merge Sort = Sorting of a list of values by recursively dividing the array into two halves, and merging them again with the smallest number first. Merging only starts when the arrays contain only one item. (O (n log(n)))
  • 
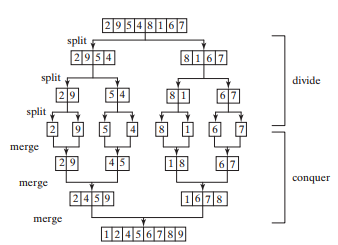
  • More efficient in the worst-case, does require more space.

• Quick Sort = Sorting of a list of values by selecting a random pivot in the array. Deviding the array into two parts so that all the elements lower then the pivot are in the first/left list, and the elements higher then the pivot are in the second/right list. On these lists is then done quick sort again. (O (n log(n)))

  • 

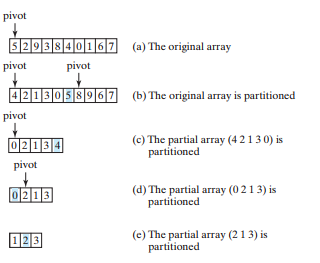
  • More space efficient then merge-sort.