8 - Binary Search Trees
8.1 - Binary Search Trees
- Binary Tree = A herarchical structure consisting of a root element with two distinct binary trees (right and left).
- Length = Number of edges in the path.
- Depth = The length of the path from the root to the specified node.
- Level = The set of nodes at a given depth.
- Siblings = Nodes that share the same parent.
- Leaf = A node without children.
- Height = The number of nodes from the root node to the most deepest node.
- Binary Search Tree (BST) = Items hich are lower than the current node is placed on the left subtree, items higher then the current node is palced on the right subtree.
A node is usually defined as follows:
class TreeNode<E> { protected E element; //Current element protected TreeNode<E> left; //Left subtree protected TreeNode<E> right; //Right subtree public TreeNode(E e) { element = e; } }
Searching for an element is done by comparing the current element (which we are looking at) with the target element (for which you are looking for).
- If the target element is smaller then the current element, go to the left subtree.
- If the target element is bigger then the current element, go to the right subtree.
- If the target element is equal to the current element, it has been found.
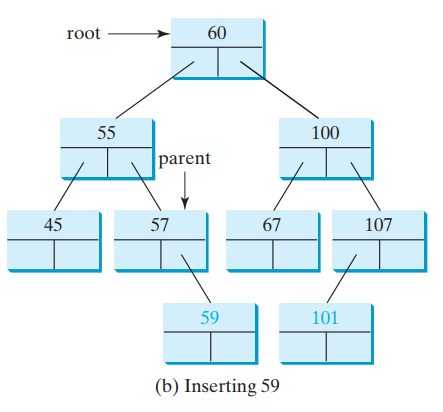
Inserting an element is done at the first parent which does not have any childs.
- While finding the parent the tree needs to be followed by comparing the element we want to insert to the one we have selected as parent.
- Moving down while keeping the rules of searching (see above) applied.
Removing an element is done by finding the element, and then if the node has a child reconnect that back to the tree.
- If the element we want to remove has a left child (see image in next paragraph):
- Replace the element to be removed with his most right (grand) child of his left subtree.
- Make any children of that most right element, children of that most rights parent.
- Example:
- We want to remove 60, he has no parent :(.
- He has child 55 and 100.
- The most right (grand)child from the left tree of 60 is 59.
- We replace 60 with 59.
- Any childs of 59 we make childs of the parent of 59 (57)
- If the element we want to remove has a right child (see image in next paragraph):
- Connect the right child of the element to be removed to the parent of that element. At the position the element to be removed was.
- Example:
- We want to remove 57, his parent is 55.
- He has child 59.
- Replace 57 with 59, and delete 57.
- If the element we want to remove has a left and a right child:
- Only do the left child removal process. Right subtree stays attached the same.
- If the element we want to remove has no childs (see image in next paragraph):
- Just take it out already.
- Example:
- We want to remove 101, his parent is 107.
- We delete 101.
- If the element we want to remove has a left child (see image in next paragraph):
You can use recusion to display binary trees.
- Using a Huffman coding scheme. Codes for characters are constructed based on the occurrence of characters in the text using a binary tree. (pg 959)
8.2 - Tree Traversal
Tree Traversal = The process of visisiting each node in the tree exactly once.
InOrder = Left - Current - Right (45, 55, 57, 59, 60, 67, 100, 101, 107)
PostOrder = Left - Right - Current (45, 59, 57, 55, 67, 101, 107, 100, 60)
PreOrder / Depth-First = Current - Left - Right (60, 55, 45, 57, 59, 100, 67, 107, 101)
Breadth-Firist = Per level, top to bottom. (60, 55, 100, 45, 57, 67, 107,59, 101)