9 - Implementing Lists, Stacks and Queues
9.1 - AVL Trees
- AVL Tree = A balanced binary tree, in which the difference in subtree heights cannot be more then 1.
- Well-balanced = The heights of every node`s two subtrees is the same.
- Balance Factor = Hight of the right subtree - hight of the left subtree .
- -1 = Tree is left heavy.
- 0 = The tree is balanced.
- +1 = The tree is right heavy.
- Complexity is O(log(n));
9.2 - Rebalancing Trees
- Rebalancing is needed if after an insertion or deletion of an element the tree becomes unbalanced (more then 1 height difference)
- Rotation = The rebalancing of a node.
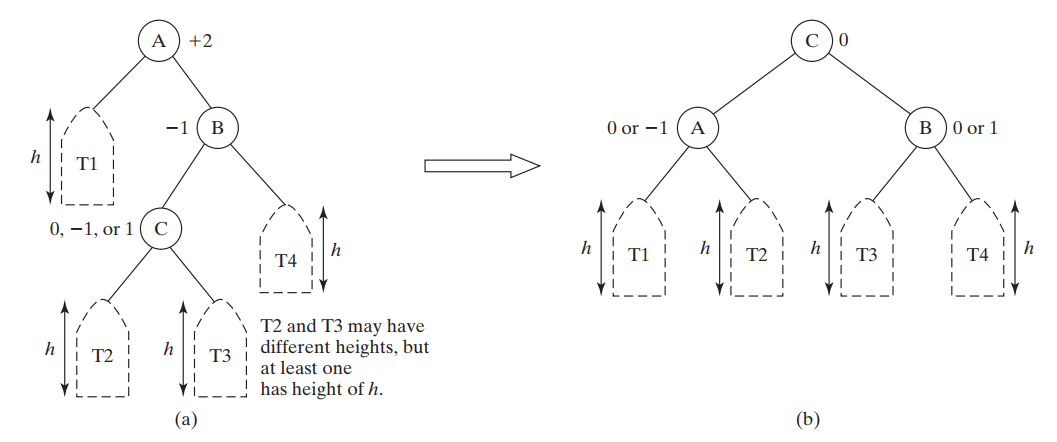
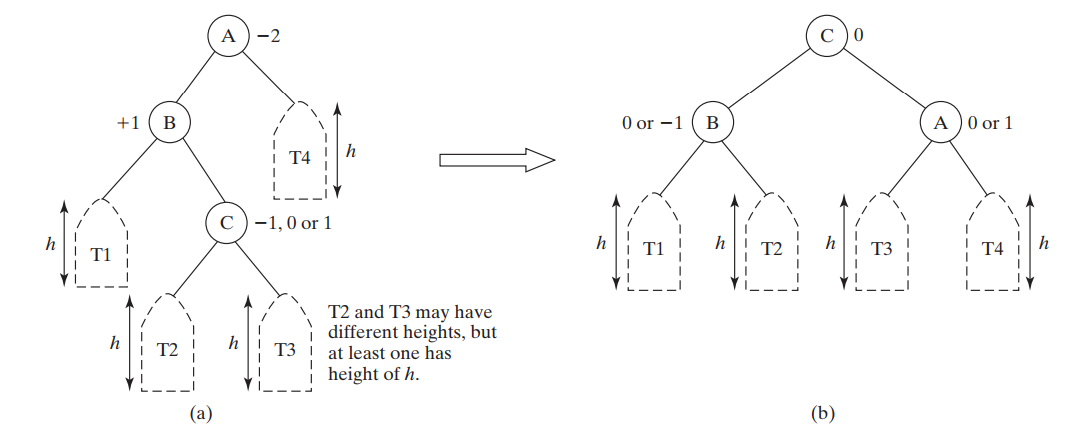
- Fixing a imbalance (letters in de brackets are for the example picture beneath):
- | | B imbalance -1 or 0 | B imbalance +1 or 0 | | :--- | :--- | :--- | | A imbalance -2 | LL Rotation = single rotation (R) | LR Rotation = double rotation (L+R) | | A imbalance +2 | RL Rotation = double rotation (R+L) | RR Rotation = single rotation (L) |
- Right rotation:
- Move A to the position of C, making C a child of A. While keeping the current subtrees in the same order.
- LL rotation example:

- Left rotation:
- Move B to the position of C, making C a child of B. While keeping the current subtrees in the same order.
- RR rotation example:

- RL rotation example:
- LR rotation example: